πの値の計算方法は、幾つも存在している。
しかし、計算方法によっては、大量の計算が必要となる、比較的少ない計算で値を出せるなどの違いがある。
分かりやすい計算方法一つに、円の中の正多角形の辺の数を増やし(正6角形から出発し、正12角形、正24角形と辺の数を増やす)、正多角形の周の長さを円の周の長さに近づけることにより、πの値を求めるものがある(資料1、2)。
pythonでプログラムを組み、πの小数点以下第10位までの正しい値(3.1415926535)を求めた。
資料1 円の中の正6角形
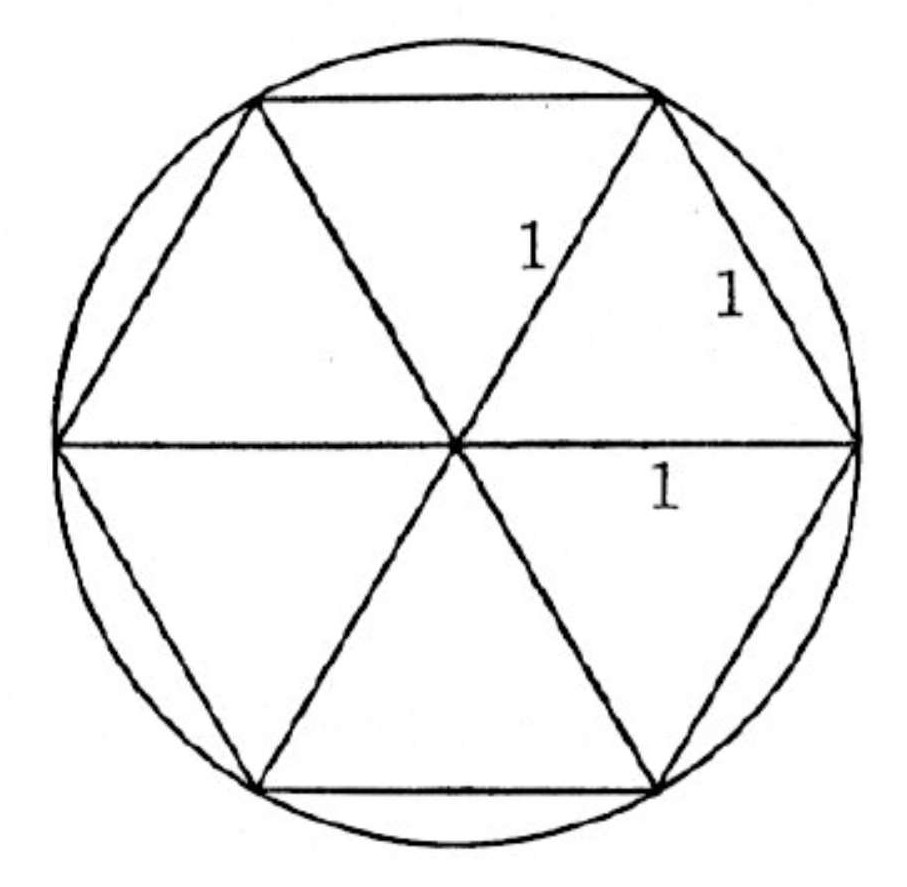
資料2 円の中の正6角形から正12角形を作図
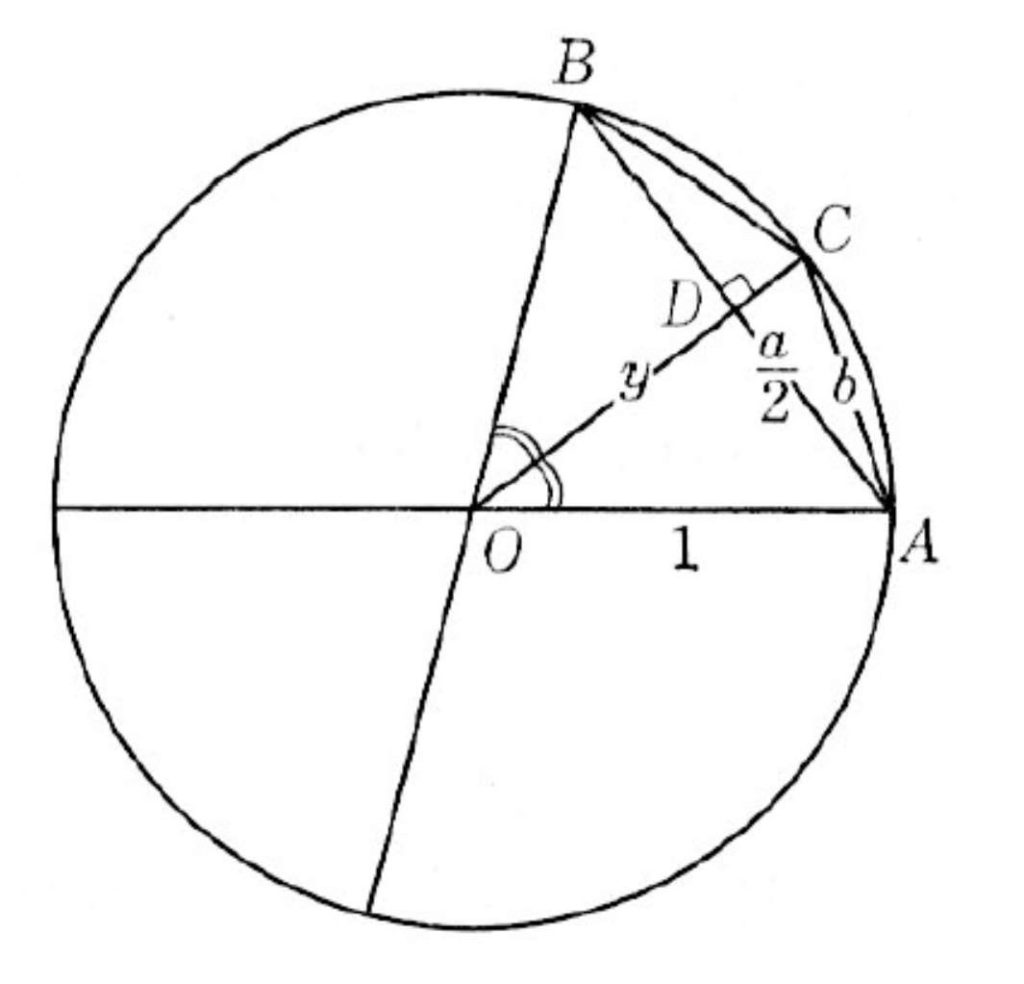
結果は、正6角形、正12角形、正24角形、…とより大きな正多角形で計算し、正393,296角形でようやく小数点以下第10位までの正しいπの値を出すことができた。
また、手持ちの資料の中に、効率的な計算と紹介されているものとしてarcsin x (sin x の逆関数)に対する級数を使うものがあった(資料3)。
資料3 arcsin x を求める級数
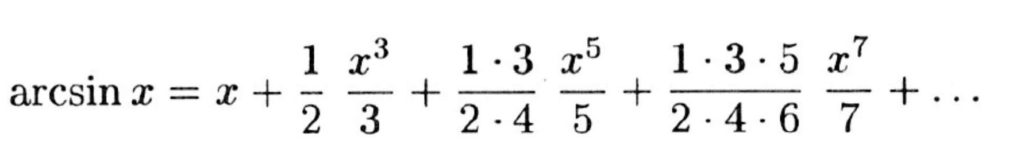
sin π/6=1/2であるから、arcsin 1/2=π/6となり、資料3にこれを代入すると、πの値を求める級数ができる(資料4)。
資料4 arcsin x の級数を使い、π/6を求める
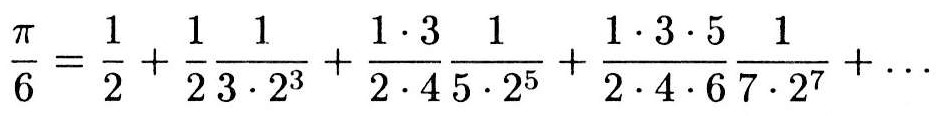
pythonでプログラムを組んだところ、資料4の級数では14番目の項まで計算することにより、小数点以下第10位までのπの正しい値を出すことができた。
コンピュータの計算ならば以上の二つの計算方法のいずれでもよいのであるが、手作業で計算するとなると、二番目の計算方法の方がはるかに計算量が少なくて済む。
今のところ、私のプログラムでは、小数点以下第15位までのπの値しか計算できない。
いずれプログラムを改良して100桁ぐらいまでπの計算を行うことを目標としたい。
