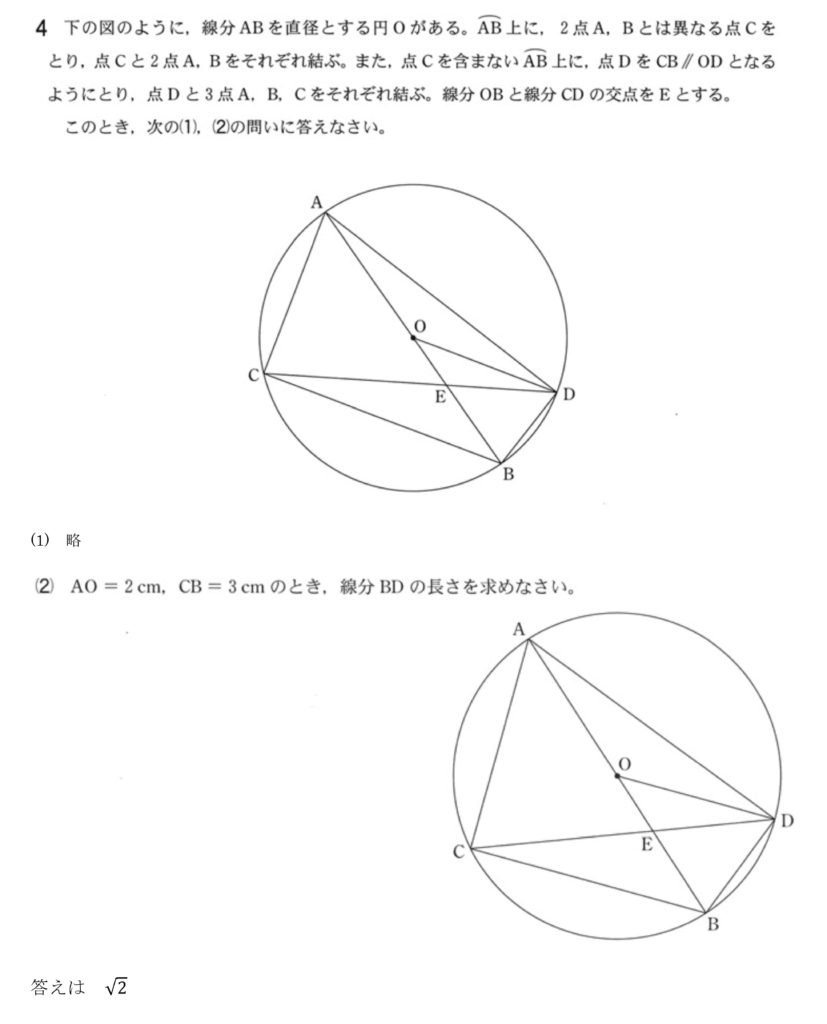
数学の二つ目の難しい問題は、大問4の(2)。
(1)で△ACDと△OBDが相似であることを証明し、それを使って線分BDの長さを求める。
相似の関係であるからAC:CD=OB:BDであり、AC、CD、OBの長さが分かれば求めるBDの長さが分かる。
まず、ACであるが、△ACBが∠ACBを直角とする直角三角形であるから、三平方の定理を使って計算することができる(AB=4、CB=3となっている)。
次に、CDであるが、これをどのようにして計算するかがこの問題を解く鍵となる。
CDを求めるには、直線DOを伸ばし、ACとの交点をFとすると、△CDFは、∠CFDを直角とする直角三角形である。
その辺FCの長さはACの二分の1である。辺DFの長さは、どのようにもとめるか。DFは、DO(半径=2)とOFの合計である。OFは、△ACBと△AFOが相似であり、相似比が2:1であることから、CB(=3)の2分の1の長さとなる。辺FCと辺DFの長さが分かったので、三平方の定理によりCDの長さを求めることができる。
OBは、半径であり、長さは2である。
後は冒頭に説明したとおり、相似比を基に方程式をつくり、BDを求めることができる。
相似比と三平方の定理を適切に使うことができるかどうかがこの問題の難しさである。