カテゴリー: 折々の記

　朝の散歩で、白鳥の元気な姿を見ました。
　どなたかが餌や水をあげているのでしょうか、橋の下の川縁の平地にバケツが置いてあり、そのそばに白鳥をよく見かけます。
　朝日を浴びてのんびりした様子。
　元気そうです。

　本日、昼前後にかけて激しい雨が降りました。
　雨がようやくあがった午後３時過ぎ、愛犬と散歩に出かけたとき、西から東の空を見上げると、大きな虹がかかっていることに気がつきました。
　天球の三分の一近くを占めたでしょうか。
　虹を久し振りに見て、こんなに大きなものなんだと思いました。

　中二生徒との勉強です（ボランティア）。

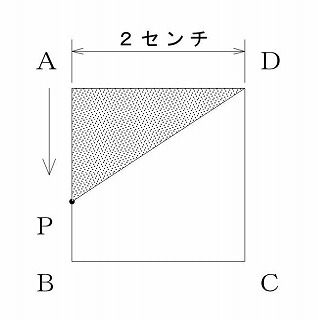
　問題は、正方形ＡＢＣＤの頂点Ａから点ＰがＢ、Ｃを通ってＤまで動くとき、三角形ＡＰＤがつくる面積ｙを一次方程式で表すことを求めるものです。
　点Ａから点Ｐまでの距離をｘと取ります。
　点Ｐが、(1)辺ＡＢの上にあるとき、(2)辺ＢＣの上にあるとき、(3)辺ＣＤの上にあるとき、と三つに分けて考えます。
　生徒は、点Ｐが辺ＡＢ、辺ＢＣの上にあるときのｙの方程式は、問題なく立てることができました。
　(1)　ｙ＝２×ｘ÷２
　(2)　ｙ＝２
　引っかかったのは、点Ｐが辺ＣＤ上にあるときです。
　三角形ＡＰＤの底辺を２センチと考え、高さＰＤをｘの文字式で表すのですが、（６－ｘ）となることが最初は飲み込めなかったようです。
　ｘは点Ｐの頂点Ａからの移動距離ですからＡからＢ、Ｃを通ってＤまでの距離は６センチですから、高さＰＤは（６－ｘ）となります。
　したがって、次の一次方程式となります。
　(3)　ｙ＝２×（６－ｘ）÷２
　　　　　　＊
　生徒は、問題文をよく読み込むことで納得しました。
　数学の問題は、国語の読解力の問題でもあると感じさせられます。

　朝の犬の散歩で、物井駅近くの文巻橋を渡ろうとしたとき、犬のさくらが立ち止まりました。
　何だろうと思って橋から下を眺めると、白鳥が鹿島川の土手で朝日を浴びながら休んでいるのが見えました（写真）。
　以前から文巻橋付近の川に浮かんでいるのをよく見かける白鳥です。
　お馴染みの近隣の方も多いと思います。
　ほぼ１年を通じてその姿を見かけます。
　外国への渡りはしないのだろうか、この近辺の鹿島川だけで十分な餌を確保できるのだろうか、１羽しか姿を見ないが、寂しくはないのだろうか、などとつい考えてしまいます。

　中学二年の生徒と、数学と英語の勉強をしました（ボランティア）。
　数学は、二元一次方程式のグラフ、つまり、ｘ－ｙ座標での直線のグラフです。
　生徒が引っかかっていた問題は、ｙ＝２ｘ－４のグラフに平行で、点（３，－４）を通る直線の式を求めなさいというものでした（方程式の数字は仮置き）。
　直線の方程式はｙ＝ａｘ＋ｂの一般式を理解できていれば、つまりａが傾き、ｂがｙ軸と交わるｙ切片と理解できていることが鍵となります。
　求める直線は、与えられた直線と平行ですから傾きは２。切片のｂを計算するために、ｙ＝２ｘ＋ｂという方程式を立て、点（３，－４）を代入してｂを計算します。
　ｂ＝－10となりますから、求める直線の方程式はｙ＝２ｘ－10。
　ｙ＝ａｘ＋ｂの一般式を理解することにより、生徒は、その他の直線のグラフや式にかかる問題はスムーズに解くことができるようになりました。

　英語について質問を受けました。
　問題文の中で”see a movie”という表現が出てきました。
　「映画を見る」ですが、生徒が知っている他の「見る」の英単語 watch は使うことができないかという質問です。
　英語は理屈で割り切ることができないことが多々あると思います。
　結局、日本語に直すと同じ意味でも、英米において日常生活の中で定着している表現が正解となると説明し、その場では watch ではなく see を使うと覚えるしかないと説明しました。
　後で辞書を引いてみると、映画館で映画を見る場合は see a movie、自宅のテレビでＤＶＤの映画を見る場合は watch a movie が普通だとあります。
　ネイティブではない外国人にとって、英語は一筋縄では行きません。

　πの値の計算方法は、幾つも存在している。
　しかし、計算方法によっては、大量の計算が必要となる、比較的少ない計算で値を出せるなどの違いがある。
　
　分かりやすい計算方法一つに、円の中の正多角形の辺の数を増やし（正６角形から出発し、正12角形、正24角形と辺の数を増やす）、正多角形の周の長さを円の周の長さに近づけることにより、πの値を求めるものがある（資料１、２）。
　ｐｙｔｈｏｎでプログラムを組み、πの小数点以下第10位までの正しい値（3.1415926535）を求めた。

資料１　円の中の正６角形

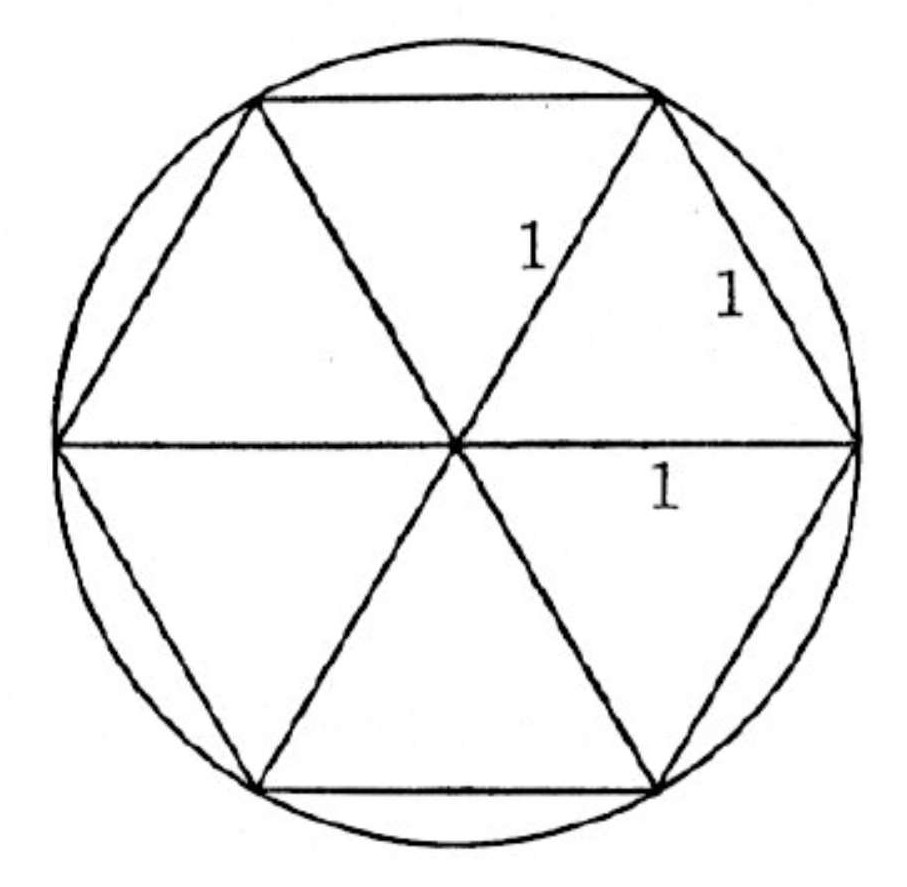
資料２　円の中の正６角形から正12角形を作図

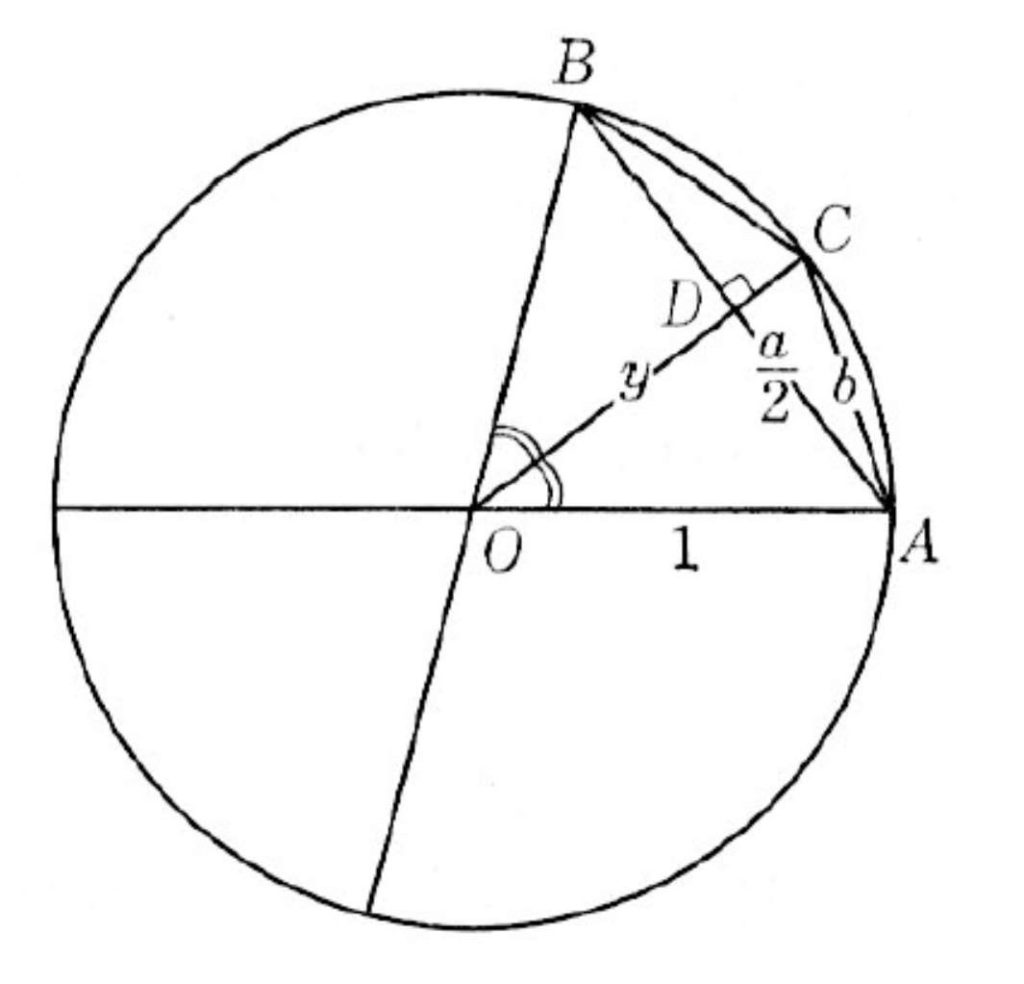
　結果は、正６角形、正12角形、正24角形、…とより大きな正多角形で計算し、正393,296角形でようやく小数点以下第10位までの正しいπの値を出すことができた。
　また、手持ちの資料の中に、効率的な計算と紹介されているものとしてarcsin x （sin x の逆関数）に対する級数を使うものがあった（資料３）。

資料３　arcsin x を求める級数

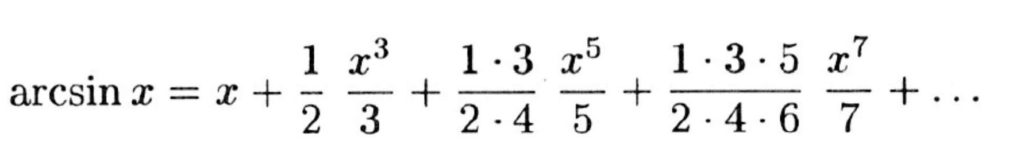
　sin π/6＝1/2であるから、arcsin 1/2＝π/6となり、資料３にこれを代入すると、πの値を求める級数ができる（資料４）。

資料４　arcsin x の級数を使い、π／６を求める

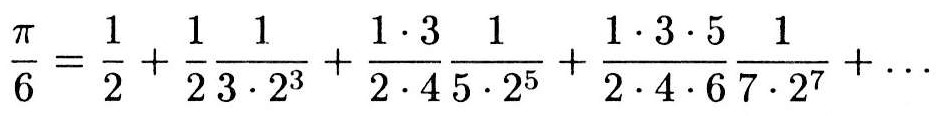
　ｐｙｔｈｏｎでプログラムを組んだところ、資料４の級数では14番目の項まで計算することにより、小数点以下第10位までのπの正しい値を出すことができた。
　コンピュータの計算ならば以上の二つの計算方法のいずれでもよいのであるが、手作業で計算するとなると、二番目の計算方法の方がはるかに計算量が少なくて済む。
　
　今のところ、私のプログラムでは、小数点以下第15位までのπの値しか計算できない。
　いずれプログラムを改良して100桁ぐらいまでπの計算を行うことを目標としたい。

　中一生徒にしばしば見られ、また、中二生徒も時折見かける演算の誤りがあります。
　括弧の外し方です。
　例：（３ｘ－７）ー（４ｘ－３）＝３ｘ－７－４ｘ＋３　となるべきところ、最後の「＋３」を「－３」としてしまい、後ろの正負記号を変えることをうっかりしている例は多いです。

　括弧の外し方に慣れてきた中二生徒でも、次のような分数の引き算の際に、やはりうっかりして正負記号を間違えることは、割合見かけます（二番目の分数の分子（2ｘ－3）は、－符号がついているので括弧を外すと－2ｘ＋3とすべきを－2ｘ－3としてしまう）。

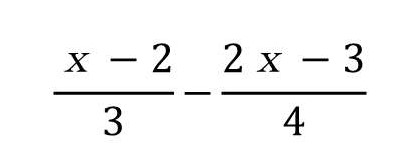
　山王公園の桜が満開となりました。
　桜は、青空によく映えます。
　私たちの心を和ませてくれます。

　いつの間にか山王公園の桜が開花していることに気がつきました。
　昨年は３月19日に開花。今年もほぼ同じ頃となりました。
　これからしばらくは、桜の花を見る楽しみに浸ることができます。

　数学以外の四教科についても一通り入試問題を解きました。

　まず英語ですが、特別に難しい問題はないように思いますが、いずれの問題も英文の問題文の内容をよく理解することができるかどうかが鍵と思われます。
　英文の内容を正確に理解することにより、初めて正しい解答を書くことができる、そんな問題が並んでいると感じます。
　その意味で、英語で高い点数をとるには、普段から英文に親しみ、英語の文章を肌身感覚で受け止めることができる、そのための幅広い経験を積んでおくことに尽きると思います。
　もちろん、リスニングや英作文も、準備が必要ですが、ただ、それほど高いレベルが求められるわけではないようです。
　英語になじみ、英語を日本語ではなく英語そのものとして理解する感覚を磨くことかなと思います。
　
　次に、国語です。
　国語は、結局文章を読み込む力が問われます。
　文章が何を言わんとしているか、的確に把握することが求められています。
　ただ、入試の文章は、それなりの内容のあるものが問題として出されます。
　もし、受験対策として国語の勉強を行うとすれば、評論や随筆などの考えさせる文章を日頃から読み込んでおくということでしょうか。
　また、漢字の読み、書き取りは必ず出題されます。ただし、それほど難度の高い問題ではないと思われますので、基礎力をしっかりつけておくことが肝要です。
　古文、漢文も必ず出題されます。
　古文の問題は、それほど難易度の高いものは出されないようですので、まずは、文章の流れと意味を理解することができるよう、普段から古文の文章に親しむことが大切でしょう。
　漢文の問題も必ず１問は出されるようです。
　今年は、返り点の打ち方でした。
　漢文については、基礎を一通り押さえておけば十分でしょう。

　次は、社会です。
　社会と理科は、難易度の高い問題が出されているとの指摘が新聞に有識者のコメントして掲載されていました。
　社会について言えば、地理の分野の資料読み取りや地図読み取りについては、今年は、それほど難しくはなかったと思います。
　問題は、歴史です。
　(1)古墳時代に朝鮮半島から日本列島に移住してきた人々を何と呼ぶか、(2)織田信長の天下統一過程における室町幕府との関係、(3)鎖国から開国に進んだときの諸事件の順序など、歴史の流れの細部まで理解していないと解答できない問題が目立ちました。
　政治・経済の分野では、経済に関する問題は、基本的なものでしたが、政治については、憲法上の新たな人権についての理解を問う問題、地方自治の直接請求権にかかる署名者数の要件などは、細部の理解が求められる問題が出され、正答を出すことが難しかったと思います。
　
　次に、理科です。
　まず、理科については、大問の数が九つと、全体的に問題数が多いとの印象があります。
　その中で注意すべき問題としては、やはり計算が必要な問題でしょうか。
　(1)図から断層のずれの大きさを読み取る問題、(2)葉と茎からの水分蒸発量を計算する問題、(3)水溶液に溶け込んだ溶質の量を計算する問題、(4)燃焼における物質の重さを求める問題、(5)滑車にかかる力を求める問題などは、計算が必要でした。
　中学校の理科は、分野が多岐にわたりますが（植物、溶解、光、音、力、地震、化学変化、呼吸、消化、動物、電流、気象、運動、遺伝、酸・アルカリ、天体など）、どの分野もきちんとした理解を持っていないと高い得点をとることが難しい科目だと思います。